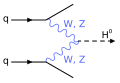Higgs Teilchen - Wikipedia
08/01/2014 01:39|
Higgs-Boson (H) |
|
|---|---|
| Klassifikation | |
| Elementarteilchen Boson |
|
| Eigenschaften | |
| Ladung | neutral |
| Masse | ca. 2,25 · 10−25 kg ca. 125–126 GeV/c2 |
| Spin | 0 |
| mittlere Lebensdauer | ca. 10-22 s |
| Wechselwirkungen | 1. Schwache Wechselwirkung 2. Wechselwirkung nach dem Higgs-Mechanismus mit allen Teilchen mit Masse 3. Schwerkraft (?) |
Das Higgs-Boson oder Higgs-Teilchen ist ein nach dem britischen Physiker Peter Higgs benanntes Elementarteilchen aus dem Standardmodell der Elementarteilchenphysik. Es ist elektrisch neutral, hat Spin 0 und zerfällt nach sehr kurzer Zeit.
Das Higgs-Teilchen gehört zum Higgs-Mechanismus, einer schon in den 1960er-Jahren vorgeschlagenen Theorie, nach der alle fundamentalen Elementarteilchen (beispielsweise das Elektron) ihre Masse erst durch die Wechselwirkung mit dem allgegenwärtigen Higgs-Feld erhalten. Für den experimentellen Nachweis des Higgs-Bosons und die Bestimmung seiner Masse sind Teilchenbeschleuniger ausreichender Energie und Luminosität nötig, weswegen der Nachweis über mehrere Jahrzehnte hinweg nicht gelang. Erst im Juli 2012 hat das Beschleunigerzentrum CERN den Nachweis eines Teilchens am Large Hadron Collider bekanntgegeben, bei dem es sich um das Higgs-Boson handeln könnte.[1] Nach Analyse weiterer Daten konnte im März 2013 die Vermutung bekräftigt werden, sie gilt aber noch nicht als endgültig bestätigt.[2]
Experten erwarten, dass die international organisierte Auswertung der bei CERN erzeugten Datenmengen sich noch über das Jahr 2013[veraltet] hinaus fortsetzen wird.[3] Jedoch gilt die experimentelle Bestätigung des ganzen Bildes als so weit fortgeschritten, dass François Englert und Peter Higgs für die theoretische Entwicklung des Higgs-Mechanismus der Nobelpreis für Physik 2013 zuerkannt wurde.[4]
Inhaltsverzeichnis
Higgs-Teilchen im Standardmodell

Die Bausteine des Standardmodells der Teilchenphysik lassen sich in vier Gruppen aufteilen: Die Quarks (die Grundbausteine der Atomkerne), die Leptonen (z. B. das Elektron), die Eichbosonen (die die Wechselwirkungen zwischen Teilchen vermitteln) und das Higgs-Feld. Durch die sogenannte zweite Quantisierung wird in der Physik der anschauliche Gegensatz zwischen Teilchen und Wellen aufgehoben, ein Teilchen wird als angeregter Zustand des entsprechenden Quantenfeldes dargestellt. Das Higgs-Boson entspricht demnach einer quantenmechanischen Anregung des Higgs-Feldes, die sich als nachweisbares Teilchen äußert. Bildhaft ausgedrückt entspricht das Higgs-Feld einer Violin- oder Gitarrensaite, als schwingungsfähigem System mit Grundzustand und Vibrationen. Das Higgs-Boson entspricht in diesem Bild dem Vibrationsmuster der Saite, die durch bestimmte Energiezufuhr in charakteristische Schwingung versetzt und damit angeregt wurde. Dies ist bei einer Saite als Ton einer bestimmten Tonhöhe hörbar. Genau dieses „In-Schwingung-Bringen der Saite“ geschieht aufgrund der erforderlichen sehr hohen Energien erst bei Kollisionen in Hochenergie-Teilchenbeschleunigern. Mit dem Nachweis des Higgs-Bosons soll auch der Nachweis für das zugrunde liegende Higgs-Feld erbracht werden.[5]
Higgs-Mechanismus
Das Higgs-Boson ist für die Teilchenphysik vor allem deshalb so wichtig, weil seine Existenz vom Higgs-Mechanismus, einem festen Bestandteil des Standardmodells, vorhergesagt wird. Die für das Standardmodell grundlegende Eichtheorie erfordert aus mathematischen Gründen, dass die Eichbosonen, die die Wechselwirkungen zwischen anderen Teilchen hervorbringen, selber Teilchen ohne Masse sind. Das ist beim Photon, dem Eichboson der elektromagnetischen Wechselwirkung, wirklich gegeben. Der Higgs-Mechanismus erklärt, wie die in der ursprünglichen Gleichung der Theorie ebenfalls masselosen Eichbosonen der schwachen Wechselwirkung (W- und Z-Bosonen) mit einem weiteren physikalischen Feld in Wechselwirkung treten und dadurch in allen weiteren Gleichungen genauso erscheinen wie Teilchen mit einer bestimmten Masse. Dieses neuartige Feld heißt Higgs-Feld. Seine elementaren Anregungen sind die Higgs-Bosonen. Die Wechselwirkung, die von den W- und Z-Bosonen ihrerseits vermittelt wird, bekommt dadurch eine kurze Reichweite, außerhalb derer sie außerordentlich schwach ist; es ist eben die „schwache Wechselwirkung“. So ermöglicht der Higgs-Mechanismus in einer grundlegenden Eichtheorie die Vereinheitlichung von elektromagnetischer und schwacher Wechselwirkung zur elektroschwachen Wechselwirkung. Darüber hinaus wird auch die Masse fermionischer Elementarteilchen (Quarks und Leptonen) durch ihre Wechselwirkung mit dem Higgs-Feld erklärt.
Die Masse, eine ursprünglich als fundamental angesehene Eigenschaft der Teilchen, wird somit als Folge einer neuen Art Wechselwirkung gedeutet.
Experimenteller Nachweis
Das Higgs-Boson hat nach den bisherigen Ergebnissen eine im Vergleich mit den meisten anderen Elementarteilchen sehr große Masse von etwa 125 GeV/c2 – das entspricht etwa zwei Eisen-Atomen (zum Vergleich: das Z-Boson hat die Masse 91 GeV/c2, das Myon 106 MeV/c2, das Elektron 511 keV/c2, das Elektron-Neutrino weniger als 2,2 eV/c2). Um die zur Erzeugung benötigte Schwerpunktsenergie aufzubringen, werden große Teilchenbeschleuniger verwendet. Wegen seiner kurzen Lebensdauer von ca 10−22 s zerfällt das Higgs-Boson praktisch am Ort des Entstehens in andere Elementarteilchen, bevorzugt in die mit der größtmöglichen Masse. In den Experimenten werden diese Zerfallsprodukte und ihre Eigenschaften gemessen und die Messwerte mit Computersimulationen des Experiments ohne und mit Higgs-Boson verglichen. Insbesondere durchsucht man die in Frage kommenden Kombinationen von Zerfallsprodukten daraufhin, ob eine bestimmte invariante Masse mit größerer Häufigkeit auftritt, als aufgrund bekannter anderer Reaktionen zu erwarten wäre. Da auch statistische Schwankungen ein solches Signal vortäuschen können, wird von der Entdeckung eines neuen Teilchens ganz allgemein erst dann gesprochen, wenn der Zufall im Mittel 3,5 Millionen oder mehr Versuche bräuchte, um (zufälligerweise!) ein derart signifikantes Ereignis zustande zu bringen (man spricht von einer Signifikanz von mindestens 5 σ).[6] Das entspricht etwa der Häufigkeit, dass beim 22-maligen Werfen einer fairen zweiseitigen Münze 22-mal „Zahl“ oben ist.
Higgs-Boson und die Ursache von Masse
In vereinfachten Darstellungen wird häufig das Higgs-Boson pauschal als Ursache von Masse dargestellt. Dies ist aus mehreren Gründen falsch bzw. unpräzise: Zum einen ist es das Higgs-Feld, das überall mit gleicher Stärke vorhanden ist und mit den Elementarteilchen des Standardmodells eine Wechselwirkung hat, durch die sie sich so verhalten, als hätten sie eine bestimmte, unveränderliche Masse. Ausgenommen sind die Photonen und Gluonen, weil sie mit dem Higgs-Feld keine Wechselwirkung haben. Weiter wird die Masse des Higgs-Bosons selbst nicht erst aus einer Wechselwirkung mit dem Higgs-Feld erklärt, sondern im Standardmodell als eine Voraussetzung angenommen, um den Higgs-Mechanismus überhaupt zu ermöglichen. Die so entstandenen Massenwerte der übrigen Teilchen tragen aber zur wägbaren Masse der gewohnten Materie, letztlich also der Masse der Atome, kaum bei, denn diese beruht nach der Äquivalenz von Masse und Energie auch auf sämtlichen Wechselwirkungen ihrer Bestandteile. Zu über 99 % steckt die Atommasse im Atomkern, dessen Masse wiederum zu etwa 99 % allein aus der starken Bindung zwischen den Quarks in seinen Nukleonen resultiert. Die durch das Higgs-Feld erzeugte Masse der Quarks selbst und der Elektronen trägt zur wägbaren Masse insgesamt nur ca. 1 Prozent bei.
Geschichte
Entwicklung der Theorie
1964 entwickelten Peter Higgs,[7][8] François Englert und Robert Brout[9] sowie Gerald Guralnik, Carl R. Hagen und Tom Kibble[10] unabhängig voneinander und ungefähr gleichzeitig denselben formalen Mechanismus, durch den zunächst masselose Elementarteilchen in Wechselwirkung mit einem Hintergrundfeld (dem „Higgs-Feld“) massiv werden. Obwohl alle drei Arbeiten hintereinander in ein und derselben Ausgabe der Fachzeitschrift Physical Review Letters erschienen, wobei Englert und Brout ihr Manuskript etwas eher eingereicht hatten, sodass ihre Veröffentlichung vor denjenigen der anderen Autoren platziert wurde, benannte man das Feld und sein Teilchen (das Feldquant) allein nach Higgs.
Der Higgs-Mechanismus wurde ursprünglich in Analogie zur Festkörperphysik entwickelt und dabei nur für abelsche Eichtheorien formuliert.[11] Nachdem er 1967 von T. W. B. Kibble auf nichtabelsche Eichtheorien (Yang-Mills-Theorien) übertragen worden war,[12] konnte der Mechanismus auf die schwache Wechselwirkung angewendet werden. Das führte zur Vorhersage der – experimentell 1983 bestätigten – großen Masse der für die schwache Wechselwirkung verantwortlichen W- und Z-Bosonen.
1968 wandte Abdus Salam[13] den Higgs-Mechanismus auf die elektroschwache Theorie von Sheldon Lee Glashow[14] und Steven Weinberg[15] an und schuf damit das Standardmodell der Teilchenphysik, wofür alle drei 1979 den Nobelpreis für Physik erhielten.
Die in populären Darstellungen,[16][17] aber nicht in der seriösen Wissenschaft verwendete Bezeichnung „Gottesteilchen“ stammt vom Nobelpreisträger Leon Max Lederman.[18][19] Ursprünglich wollte Ledermann sein Buch unter dem Titel The goddamn particle („Das gottverdammte Teilchen“) veröffentlichen. Sein Verleger zwang ihn jedoch, den Titel zu ändern, sodass das Buch 1993 unter einem anderen Titel erschien: The God Particle: If the Universe Is the Answer, What Is the Question? („Das Gottesteilchen: Wenn das Universum die Antwort ist, was ist die Frage?“)[20]
Peter Higgs selbst lehnte den Ausdruck Gottesteilchen ab, da er religiöse Menschen verletzen könne.[21]
Experimentelle Suche
Überblick
-
Zwei Gluonen erzeugen je ein Top/Antitop-Quark-Paar, die zu einem Higgs-Boson kombinieren.
-
Zwei Quarks emittieren W- oder Z-Bosonen, die zu einem Higgs-Boson kombinieren.
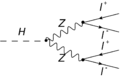
Die obenstehenden Abbildungen zeigen in Form von Feynman-Diagrammen links zwei Mechanismen, nach denen ein Higgs-Boson am LHC produziert werden könnte. Rechts sind zwei mögliche Zerfallswege („Zerfallskanäle“) für Higgs-Bosonen dargestellt. Der Zerfall eines Higgs-Bosons in zwei Photonen führt dazu, dass in einem Beschleunigerexperiment gegenüber einem Modell ohne Higgs-Boson mehr Photonenpaare mit einer Schwerpunktsenergie oder invarianten Masse gleich der Masse des Higgs-Bosons erzeugt werden. Da das Higgs-Boson selbst nicht mit Photonen wechselwirkt, muss der Zerfall über intermediäre elektrisch geladene Teilchen (im obigen Diagramm über ein geladenes Fermion  ) erfolgen. Der Zerfall eines Higgs-Bosons in vier elektrisch geladene Leptonen mittels intermediärer Z-Bosonen zählt zusammen mit dem Zerfall in zwei Photonen zu den wichtigen Entdeckungskanälen für das Higgs-Boson. Durch systematisches kombiniertes Suchen nach diesen Zerfällen konnten an zwei unabhängigen Detektoren des LHC deutliche Hinweise auf die Existenz eines entsprechenden Teilchens gefunden werden. Die lokale Signifikanz beträgt hierbei 5,9 σ, was einen Irrtum bei der Entdeckung weitestgehend ausschließt.[22][23]
) erfolgen. Der Zerfall eines Higgs-Bosons in vier elektrisch geladene Leptonen mittels intermediärer Z-Bosonen zählt zusammen mit dem Zerfall in zwei Photonen zu den wichtigen Entdeckungskanälen für das Higgs-Boson. Durch systematisches kombiniertes Suchen nach diesen Zerfällen konnten an zwei unabhängigen Detektoren des LHC deutliche Hinweise auf die Existenz eines entsprechenden Teilchens gefunden werden. Die lokale Signifikanz beträgt hierbei 5,9 σ, was einen Irrtum bei der Entdeckung weitestgehend ausschließt.[22][23]
Resultate
Da sich viele spezielle Eigenschaften einer solchen elektroschwachen Wechselwirkung experimentell sehr gut bestätigt haben, gilt das Standardmodell mit einem Higgs-Teilchen als plausibel. Nach dem Standardmodell und Experimenten mit anderen Teilchen sollte die Masse des Higgs-Bosons, sofern es existiert, höchstens 200 GeV/c2 sein. (Zum Vergleich: Proton und Neutron haben je rund 1 GeV/c2.) Wäre in diesem Bereich kein Higgs-Teilchen gefunden worden, sagten einige Theorien ein Higgs-Multiplett vorher, welches auch bei höheren Energien realisiert sein könnte.
Bereits 2003 konnten Datenauswertungen am LEP am CERN 114,4 GeV/c2 als Untergrenze für die Masse ermitteln.[24] Zusätzlich konnte bei Messungen der CDF- und D0-Experimente (2010) am Tevatron von Fermilab der Bereich 156–175 GeV/c2 ausgeschlossen werden.[25][26]
Im Dezember 2011 und Februar 2012 wurden vorläufige Berichte der Experimente am LHC des CERN veröffentlicht, wonach die Existenz eines Standard-Modell-Higgs-Bosons in verschiedenen Massenbereichen mit hohen Konfidenzniveaus ausgeschlossen werden konnte. Hierbei wurden Daten aus 2011 von Teilchenkollisionen mit Energien von ungefähr 7 TeV ausgewertet. Gemäß diesen Resultaten liegt die Masse des Higgs-Bosons, falls es existieren sollte, im Bereich von 116–130 GeV/c2 (ATLAS[27]) bzw. 115–127 GeV/c2 (CMS[28]). Dabei konnten erste Anzeichen für die Existenz des Teilchens gewonnen werden. Bei diesen Detektionen wurde eine Masse von 124 bis 126 GeV/c2 mit einer lokalen Signifikanz von über 3 σ gemessen.[29] Für die Anerkennung als wissenschaftliche Entdeckung in der Teilchenphysik sind allerdings mindestens 5 σ erforderlich.[30] Im Juli ergab eine weitere Analyse der 2011-Daten durch ATLAS eine lokale Signifikanz von 2,9 σ bei ungefähr 126 GeV/c2.[31]
Auch die CDF- und DØ-Gruppen des inzwischen stillgelegten Tevatron lieferten im März und Juli 2012 neue Datenauswertungen, die mögliche Hinweise auf das Higgs-Boson im Bereich 115–135 GeV/c2 enthielten, mit einer Signifikanz von 2,9 σ.[32][33]
Am 4. Juli 2012 veröffentlichten die LHC-Experimente ATLAS und CMS Ergebnisse, wonach ein Teilchen mit einer Masse von 125–127 GeV/c2 gefunden wurde.[1] Hierbei wurden zusätzlich Daten aus 2012 von Teilchenkollisionen mit Energien von ungefähr 8 TeV ausgewertet. Die lokale Signifikanz erreichte bei beiden Experimenten 5 σ, wobei die Einbeziehung weiterer Kanäle bei CMS die statistische Signifikanz des angegebenen Wertes leicht reduzierte (4,9 σ). Die Massen des neuen Teilchens ergaben sich zu ∼126,5 GeV/c 2 (ATLAS),[34][35] und 125,3 ± 0,6 GeV/c2 (CMS).[36][37]
Am 31. Juli 2012 verbesserte ATLAS die Datenanalyse durch Einbeziehung eines weiteren Kanals und erhöhte so die Signifikanz auf 5,9 σ bei einer Masse von 126 ± 0,4 (stat) ± 0,4 (sys) GeV/c2.[38] Ebenso erhöhte CMS die Signifikanz auf 5 σ bei einer Masse von 125,3 ± 0,4 (stat) ± 0,5 (sys) GeV/c2.[39]
Um sicherzustellen, dass das gefundene Teilchen tatsächlich das Higgs-Boson des Standardmodells ist, müssen weitere Daten gewonnen und ausgewertet werden. Insbesondere muss für das gefundene Teilchen untersucht werden, mit welchen Häufigkeiten die verschiedenen möglichen Kombinationen anderer Teilchen auftreten, in die es zerfällt. Für das Higgs-Boson gilt nämlich eine spezifische Voraussage: Die Wahrscheinlichkeit, beim Zerfall ein Teilchen zu erzeugen, steigt proportional zum Quadrat der Masse des Teilchens. Im November 2012 wurden von der ATLAS- und der CMS-Kooperation Ergebnisse zu fünf verschiedenen Zerfallskanälen veröffentlicht[40][41] (Zerfall in (1) zwei Gammaquanten, (2) vier Elektronen oder Myonen, (3) zwei Elektronen/Myonen und zwei Neutrinos, (4) zwei  -Leptonen, oder (5) zwei Bottom-Quarks). Sie widersprechen den Voraussagen des Standardmodells nicht, sind aber noch mit zu großen Unsicherheitsbereichen behaftet, als dass eine endgültige Bestätigung gefolgert werden könnte.
-Leptonen, oder (5) zwei Bottom-Quarks). Sie widersprechen den Voraussagen des Standardmodells nicht, sind aber noch mit zu großen Unsicherheitsbereichen behaftet, als dass eine endgültige Bestätigung gefolgert werden könnte.
M. Schumacher und C. Weiser schrieben in einem Artikel einer Physik-Zeitschrift[42] im August 2012: „Die Entdeckung eines Higgs-artigen Teilchens nach jahrzehntelangen Anstrengungen ist ein Meilenstein der Physik, unabhängig davon, ob es sich letztendlich als das Higgs-Boson des Standardmodells, das einer erweiterten Theorie oder etwas völlig Unerwartetes erweist.“
Im März 2013 stellten ATLAS und CMS neue Analysen vor, die bestätigen, dass das neue Teilchen mit den Vorhersagen für das Higgs-Boson kompatibel ist.[2]
Higgs-Bosonen außerhalb des Standardmodells
Im minimalen supersymmetrischen Standardmodell (MSSM), einer Erweiterung des Standardmodells für die Supersymmetrie, gibt es fünf Higgs-Bosonen, drei „neutrale“ und zwei „geladene“ (die Begriffe „neutral“ bzw. „geladen“ sind dabei wie in der elektroschwachen Eichtheorie definiert):
| enthalten in … | Masse | Elektrische Ladung | Symm.eigenschaft | |
|---|---|---|---|---|
| neutral | geladen | |||
| Standardmodell (Higgs-Boson) |
rel. leicht |  |
– | Skalar |
| MSSM | schwer |  |
 |
|
 |
– | Pseudoskalar | ||
Das A-Teilchen ist ungerade bzgl. der CP-Symmetrie, d. h. es ist ein Pseudoskalar, während das h- und das H-Boson CP-gerade sind (Skalare). Außerdem koppelt das A-Teilchen nicht an die drei Eichbosonen W+, W− bzw. Z.
Das h-Boson hat abhängig vom benutzten Benchmark-Szenario eine theoretisch erlaubte Masse von maximal 133 GeV/c2 und gilt daher als besonders ähnlich zum Higgs-Boson des Standardmodells.[43][44]
Zu diesen fünf Higgs-Bosonen werden in diesem Modell als Superpartner noch fünf weitere, sogenannte Higgsinos  postuliert.
postuliert.
Literatur
- Gordon Kane: Das Higgs-Teilchen. Das Geheimnis der Masse. In: Spektrum der Wissenschaft. Heidelberg 2006, Nr. 2, ISSN 0170-2971, S. 36–43.
- John F. Gunion, Sally Dawson, Howard E. Haber: The Higgs Hunter’s Guide. Perseus Publ., Cambridge Mass 2000, ISBN 0-7382-0305-X.
- Walter Greiner: Eichtheorie der schwachen Wechselwirkung. Thun, Frankfurt am Main 1995, ISBN 3-8171-1427-3, S. 133 ff..
Einzelnachweise und Kommentare
- ↑ Hochspringen nach: a b CERN experiments observe particle consistent with long-sought Higgs boson. Pressemitteilung von CERN. 4. Juli 2012. Abgerufen am 15. Oktober 2012.
- ↑ Hochspringen nach: a b New results indicate that particle discovered at CERN is a Higgs boson. Pressemitteilung von CERN. 14. März 2013. Abgerufen am 14. März 2013.
- Hochspringen ↑ Ein Beispiel für die noch bevorstehenden und auch durch die vorangehende Referenz nicht überholten Diskussionen findet sich in der Ankündigung einer öffentlichen „Expertenrunde“, die Mitte Februar 2013 im Rahmen des Meetings der AAAS stattfand.
- Hochspringen ↑ Nobelprize.org: The Nobel Prize in Physics 2013, abgerufen am 8. Oktober 2013.
- Hochspringen ↑ M. Strassler: The Standard Model Higgs. In: „Of Particular Significance“ (Blog). 13. Dezember 2011, abgerufen am 15. Juli 2012 (englisch).
- Hochspringen ↑ Beitrag von David Spiegelhalter zum Zahlenwert 1 : 3,5 Mio. als Reaktion auf eine falsche Darstellung in einem Nature-Artikel zur Higgs-Teilchen-Suche. Die enorm große Zahl 3,5 Millionen ist der Kehrwert der weiter unten genannten sehr kleinen Zahl p; 5,0 σ entspricht p=2,8x10-7.
- Hochspringen ↑ P. W. Higgs: Broken symmetries, massless particles and gauge fields. In: Phys. Lett.. 12, 1964, S. 132. doi:10.1016/0031-9163(64)91136-9.
- Hochspringen ↑ P. W. Higgs: Broken symmetries and the masses of gauge bosons. In: Phys. Rev. Lett.. 13, 1964, S. 508. doi:10.1103/PhysRevLett.13.508.
- Hochspringen ↑ F. Englert, R. Brout: Broken symmetry and the mass of gauge vector mesons. In: Phys. Rev. Lett.. 13, 1964, S. 321. doi:10.1103/PhysRevLett.13.321.
- Hochspringen ↑ G. S. Guralnik, C. R. Hagen, T. W. B. Kibble: Global conservation laws and massless particles. In: Phys. Rev. Lett.. 13, 1964, S. 585. doi:10.1103/PhysRevLett.13.585.
- Hochspringen ↑ Bei den sogenannten abelschen Gruppen wird angenommen, dass es – wie bei der Multiplikation zweier reeller Zahlen – bei der Hintereinanderausführung zweier Gruppenelemente a bzw. b nicht auf die Reihenfolge ankommt, a x b = b x a. Für nichtabelsche Gruppen trifft dies nicht zu.
- Hochspringen ↑ T. W. B. Kibble: Symmetry breaking in non-Abelian gauge theories. In: Phys. Rev.. 155, 1967, S. 1554. doi:10.1103/PhysRev.155.1554.
- Hochspringen ↑ A. Salam: Weak and electromagnetic interactions. In: Proc. Nobel Symp.. 8, 1968, S. 367–377.
- Hochspringen ↑ S. L. Glashow: Partial symmetries of weak interactions. In: Nucl. Phys.. 22, 1961. doi:10.1016/0029-5582(61)90469-2.
- Hochspringen ↑ S. Weinberg: A model of leptons. In: Phys. Rev. Lett.. 19, 1967. doi:10.1103/PhysRevLett.19.1264.
- Hochspringen ↑ Higgs-Boson: Hoffen auf das Gottesteilchen – Artikel bei Spiegel online, vom 7. Dezember 2011
- Hochspringen ↑ Teilchenbeschleuniger LHC: Warum nennt man das Higgs-Boson auch »Gottesteilchen«? – Artikel (Seite 2/2 in Im Trommelfeuer der Urknälle) bei Zeit online, vom 7. April 2010
- Hochspringen ↑ https://faculty.washington.edu/lynnhank/Lederman2.pdf S. 2
- Hochspringen ↑ Anything but the God particle. The Guardian. 29. Mai 2009. Abgerufen am 6. Juli 2012.
- Hochspringen ↑ James Randerson: Father of the ’God Particle’. In: The Guardian, 30. Juni 2008.
- Hochspringen ↑ „Interview: the man behind the ’God particle'“, New Scientist 13 September, 2008, pp. 44–5
- Hochspringen ↑ 5,9 σ entspricht einem sog. p-Wert von ~10-9 (siehe eine weiter oben auffindbare Fußnote); 5,0 σ einem p-Wert von 2,8x10-7.
- Hochspringen ↑ Eine sehr suggestive Auftragung über zehn Masse-Dekaden, für den gesamten Bereich von 110 bis 150 GeV/c2, findet sich in einem Artikel von Markus Schumacher und Christian Weiser, Higgs- oder nicht Higgs-Boson?, Physik Journal 11 (8/9), 2012, S. 18–20, Abb. 2. Anmerkung zu dieser Abbildung: Allerdings besitzen die bei beiden Detektoren beobachteten enorm tiefen „Tröge“ für die Masse des neuen Teilchens zugleich eine nicht zu vernachlässigende Breite (d. h. es ist nicht sinnvoll, die Masse des neuen Teilchens extrem scharf anzugeben; zusätzlich ist vielmehr ein Wert für die Ungenauigkeit der Massenbestimmung nötig).
- Hochspringen ↑ LEP Working Group For Higgs Boson Searches: Search for the Standard Model Higgs boson at LEP. In: Physics Letters B. 565, 2003, S. 61-75. arXiv:hep-ex/0306033. doi:10.1016/S0370-2693(03)00614-2.
- Hochspringen ↑ Fermilab experiments narrow allowed mass range for Higgs boson. Fermilab. 26. Juli 2010. Abgerufen am 28. April 2012.
- Hochspringen ↑ The CDF & D0 Collaborations: Combined CDF and D0 Upper Limits on Standard Model Higgs Boson Production with up to 8.6 fb-1 of Data. 2011. arXiv:1107.5518.
- Hochspringen ↑ ATLAS Collaboration: Combined search for the Standard Model Higgs boson using up to 4.9 fb-1 of pp collision data at s=7 TeV with the ATLAS detector at the LHC. In: Physics Letters B. 710, Nr. 1, 2012, S. 49–66. arXiv:1202.1408. doi:10.1016/j.physletb.2012.02.044.
- Hochspringen ↑ CMS Collaboration: Combined results of searches for the standard model Higgs boson in pp collisions at s=7 TeV. In: Physics Letters B. 710, Nr. 1, 2012, S. 26-48. arXiv:1202.1488. doi:10.1016/j.physletb.2012.02.064.
- Hochspringen ↑ ATLAS and CMS experiments submit Higgs search papers. CERN press release. 7. Februar 2012. Abgerufen am 28. April 2012.
- Hochspringen ↑ Seife, C.: CERN’s gamble shows perils, rewards of playing the odds. In: Science. 289, Nr. 5488, 2000, S. 2260–2262. doi:10.1126/science.289.5488.2260.
- Hochspringen ↑ ATLAS Collaboration: Combined search for the Standard Model Higgs boson in pp collisions at sqrt(s) = 7 TeV with the ATLAS detector. In: Physical Review D. 86, Nr. 3, 2012, S. 032003. arXiv:1207.0319. doi:10.1103/PhysRevD.86.032003.
- Hochspringen ↑ Tevatron scientists announce their final results on the Higgs particle. Fermilab press room. 2. Juli 2012. Abgerufen am 2. Juli 2012.
- Hochspringen ↑ The CDF & D0 Collaborations: Updated Combination of CDF and D0 Searches for Standard Model Higgs Boson Production with up to 10.0 fb-1 of Data. 2012. arXiv:1207.0449.
- Hochspringen ↑ Latest Results from ATLAS Higgs Search. ATLAS. 4. Juli 2012. Abgerufen am 4. Juli 2012.
- Hochspringen ↑ ATLAS collaboration: Observation of an Excess of Events in the Search for the Standard Model Higgs boson with the ATLAS detector at the LHC. In: ATLAS-CONF-2012-093. 2012.
- Hochspringen ↑ Observation of a New Particle with a Mass of 125 GeV. CMS. 4. Juli 2012. Abgerufen am 4. Juli 2012.
- Hochspringen ↑ CMS collaboration: Observation of a new boson with a mass near 125 GeV. In: CMS-PAS-HIG-12-020. 2012.
- Hochspringen ↑ ATLAS collaboration: Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC. In: Physics Letters B. 716, Nr. 1, 2012, S. 1-29. arXiv:1207.7214. doi:10.1016/j.physletb.2012.08.020.
- Hochspringen ↑ CMS collaboration: Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. In: Physics Letters B. 716, Nr. 1, 2012, S. 30-61. arXiv:1207.7235. doi:10.1016/j.physletb.2012.08.021.
- Hochspringen ↑ Higgs Property Measurement with ATLAS, S. 15
- Hochspringen ↑ Grafische Aufbereitung der Ergebnisse
- Hochspringen ↑ M. Schumacher und C. Weiser., Higgs- oder nicht Higgs-Boson?, Physik Journal 11 (8/9), S. 18–20, 2012
- Hochspringen ↑ David Eriksson: H±W∓ production at the LHC. High Energy Physics, Uppsala University, IKP seminar, 6. Oktober 2006 (PDF).
- Hochspringen ↑ Janusz Rosiek: Complete Set of Feynman Rules for the MSSM – inkl. erratum. 6. November 1995, KA-TP-8-1995, hep-ph/9511250 hep-ph/9511250, doi:10.1103/PhysRevD.41.3464.